Some topics in scattering and resonance

Contents

1. Metamaterials: artificial bulk material properties from high-contrast fine structure

• Artificial magnetism

• Convergent power series for waves in metamaterials

2. Guided modes in periodic structures and transmission anomalies

• Modes guided by a periodic slab; Fano resonance in photonic structures.

• Modes guided by a planar defect in a photonic crystal

3. Calderón boundary-integral projectors

• Homogeneous media and application to guided modes and scattering

• Periodic media and application to thick photonic crystal slabs and spectral gaps

4. Boundary-integral numerical code

5. Optimization

• Manipulation of transmission

• Density of states for photonic crystal slabs

6. Transmission gaps and anomalies

• Complete and incomplete spectral gaps

• Defects and transmission anomalies

Periodic channel

Fabry-Perot mirror

Surface defect

Random crystals

1. Metamaterials: artificial bulk material properties from high-contrast fine structure

Artificial magnetism

In 1999, John Pendry and others introduced periodic arrays of microresonators as a means of creating magnetism at frequencies for which magnetic response does not occur naturally. The components of the composite are in themselves non-magnetic, and it is the resonance at the fine scale of the resonators that produces magnetic activity. The idea is that the combination of high conductivity and small ratio between the period of the array to the bulk variation of the electromagnetic fields causes a discontinuity in the magnetic field at the edges of the resonators. See the references in [KoSh08], in which we rigorously analyze a 2D model using two-scale homogenization. See also the work of Bouchitté and Schweizer on a 3D model referenced in the same work.

Artificial magnetism can also be created by high-contrast dielectric rods arranged periodically in a neutral host. In the homogeneous limit, a sequence of spectral bands and gaps emerges. See the works of Zhikov, Hempel/Lienau, and Bouchitté/Felbacq referenced in [FLS10ab].

Convergent power series for waves in metamaterials

In formal homogenization of periodically micro-structured media, one expands fields in formal power series with respect to the small cell size. For a finite sample of the composite, one cannot expect the power series to converge to a field in the medium for any non-zero cell size because of boundary effects. But for Bloch waves in infinite high-contrast media, one can prove convergence. This has been done for the two types of meta-material described above in [FSL10b] and [Sh10b]. It even works with a negative material coefficient in the inclusions (the analysis is in fact easier in that case). Thus one actually proves existence of solutions, near but not at the homogenization limit for noncoercive problems!

In certain cases, one can even quantitatively calculate a radius of convergence of these power-series representations of waves and thus obtain a way to compute the fields in specific structures to arbitrary algebraic order of accuracy in the cell-to-wavelength ratio. This analysis was done for plasmonic inclusions (with large negative frequency-dependent index) in the dissertation of Santiago Fortes (Louisiana State University 2009) and in [FLS10a] by using fine properties of the Catalan numbers, which are defined recursively through convolution:

C₀ = 1,
C_n+1 = ∑ⁿ_j=0 C_n-j C_j.

2. Guided modes in periodic structures and transmission anomalies

Modes guided by a periodic slab

Modes guided by a planar defect in a photonic crystal

If we reverse the roles of the periodic structure and the air, then we have a planar waveguide in a photonic (or acoustic) crystal. Guided modes may exist in the air at frequencies that are in a spectral gap for the perfect periodic structure. See Refs. 2 (Ammari/Santosa) and 10 (Kuchment/Ong) in [RaSh08] in my list of articles. These modes are understood to cause resonant scattering behavior when a crystal with a planar waveguide, truncated parallel to the guide, is illuminated by a plane wave. Some simulations of this resonant scattering behavior are shown in the part of Section 5 of this page called "Fabry-Perot mirror". Detailed numerical calculations of resonant transmission spikes are shown in Ref. 15 of [RaSh08].

In [RaSh08], we prove that a spectral gap emerges as an interval of zero transmission of energy through a thick slab of a periodic material as the thickness tends to infinity. We also prove that transmission anomalies occur at guided mode frequencies for one-dimensional structures. We employ the Calderón boundary-integral projectors based on the radiating Green function for the Helmholtz equation in free space and the decaying Green function for the Helmholtz equation in a periodic structure.

3. Calderón boundary-integral projectors

The Calderón boundary-integral projectors for elliptic differential operators are analogous to the Cauchy boundary-integral projections in the theory of complex variables. There, an arbitrary function defined on a curve that divides the complex plane into two domains is decomposed uniquely into the boundary value of a holomorphic function on one side of the curve plus the boundary value of a holomorphic function on the other side, with both functions decaying like 1/z as z→∞ (unless one of the domains is bounded). These projections are (I ± H), where H is the Hilbert transform on the boundary, and the identity I arises from the Sokhotskyi-Plemelj formula.

There is a similar decomposition involving, say, Helmholtz or Maxwell fields in two domains separated by an interface. The projections, called the Calderón projectors, involve single- and double-layer potentials of an appropriate Green function (analogous to the Cauchy kernel 1/(z-z₀). The choice of the Green function depends on the application. The reader is referred to Refs. 5 (Costabel/Stephan) and 11 (Nédélec) in [ShVe03] for the projectors for the Helmholtz and Maxwell equations associated with a bounded scatterer.

Homogeneous media and application to guided modes and scattering

The Calderón projectors provide a natural and beautiful way to pose the problem of scattering of plane waves by an obstacle. This could be, say, a bounded obstacle in free space, a bounded obstacle in a wave-guide, or a periodic slab. In [ShVe03], we show how to formulate the problem in the case of a periodic slab and use the properties of the projectors to gain knowledge about guided modes. The idea of the formulation of the scattering problem is this: The total field on the boundary of the scatterer together with its normal derivative (its trace) have values coming from the interior of the scatterer and values coming from the exterior, and these value must be matched appropriately. Both interior and exterior traces are decomposed into traces of the source and scattered fields. In the interior, this decomposition coincides with the decomposition arising from the complementary Calderón projectors constructed from a Green function with the interior material properties, and in the exterior, it coincides with the decomposition arising from the projectors that use the radiating Green function with the exterior material properties. Projecting onto the traces of the (known) source fields in the exterior and interior gives an equation of the form (B + C)u = f, where B is bounded, C is compact, u is the trace of the total field, and f is essentially the trace of the sum of the source fields.

Seeing that B and C depend analytically on the frequency ω and the Bloch wave vector κ parallel to the slab, the equation (B + C)u = 0 gives rise to a complex dispersion relation between κ and ω corresponding to generalized guided modes of the slab. Real-valued pairs (κ,ω) correspond to true guided modes. Since the imaginary part of ω on the dispersion relation must be negative, typical pairs correspond to fields that are decaying in time but exponentially growing spatially with distance from the slab. These are analogous to the fields of the "scattering resonances" for the Helmholtz resonator; see Ref. 6 (J. T. Beale) of [ShVe03].

Periodic media and application to thick photonic crystal slabs and spectral gaps

In [RaSh08], we extend the Calderón projectors to interfaces between two complementary subdomains of a periodic medium. We then use these to investigate the limiting behavior of transmission of harmonic fields at frequencies in a spectral gap of the medium.

4. Boundary-integral numerical code

For the simulations of fields in periodic slabs that you see on this page, we used a numerical code developed at Duke University by M. Haider, S. Shipman, and S. Venakides [HaShVe02]. It is based on the integral representations that are formulated most elegantly using the Calderón boundary-integral projectors mentioned above [ShVe03].

The algorithm uses an acceleration technique that is similar to a multipole algorithm, specialized to periodic structures. Most efficiency is gained when the number of periods across the slab is very large. References on multipole algorithms can be found on the website of L. Greengard.

5. Optimization

Manipulation of transmission

In [LiShVe03], we develop the variational calculus for the transmission coefficient as a function of the material parameters ε and μ for two-dimensional scattering of electromagnetic plane waves by periodic slabs. The L^p theory of the variational calculus is made rigorous in [Sh08]. The simulations below show how transmission features can be optimized with the resulting gradient-flow algorithm.

Perfect square lattice with no channel


Perfect square lattice with a channel every three rows


Perturbed lattice with channels


Intensity of the scattered field at the frequency of the peak transmission above



Moving a transmission gap

Density of states for PC slabs

I have implemented an algorithm for optimizing the "effective density of states" for a photonic crystal slab. This effective density is discussed in [Bendickson/Dowling/Scalora, Phys. Rev. E, 53 No. 4 p. 4107]. It is essentially the sensitivity of the effective wave number of a scattered field across the slab with respect to frequency and is thus directly related to the phase of the complex transmission coefficient. Anomalous behavior of this quantity coincides with resonant scattering in the structure and anomalous transmission of energy (the magnitude of the transmission coefficient).

6. Transmission gaps and resonant transmission: Simulations

Complete and incomplete spectral gaps

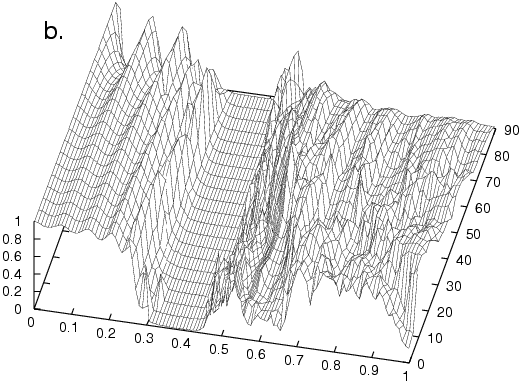
Graph (a) below shows the transmission of energy through an infinite slab of a square-lattice photonic crystal of circular rods, five rods thick, as a function of reduced frequency (from 0 to 1) and angle of incidence (from 0° to 90°).

Notice the complete gap from frequencies of about 0.3 to 0.45 and the incomplete gap around 0.6. Graphs (b), (c), and (d) show realizations of how the transmission changes under random perturbations of the centers of the five rods in a period (the structure remains periodic---the perturbations are the same in each period). In (b), the perturbations are taken to uniformly distributed up to 10% of the distance between adjacent rods, in (c), it is 20% and in (d) it is 30%.

Observe that the complete gap is robust under these perturbations, whereas the incomplete gap is not.

Defects and transmission anomalies

Perfect 6x4 supercell

1. (1.54)

2. (1.99)

6x4 supercell with a channel of width d=0.25 relative to the period after each 6 rows (seen in the images at the top of the supercell)

1. (1.62)	2. (137.1)
3. (2.05)	4. (2.77)

6x4 supercell with a channel of width d=0.5

1. (1.67)	2. (108.2)
3. (2.10)	4. (3.70)

6x4 supercell with a channel of width d=0.5

1. (1.54)	2. (1.76)	3. (108.2)
4. (61.2)	5. (2.09)	6. (2.67)
7. (10.5)	8. (2.26)	9. (3.70)
10. (2.24)	11. (2.23)	12. (2.22)

Fabry-Perot mirror

Scattering by a Fabry-Perot photonic crystal mirror.


Transmission through a Fabry-Perot photonic crystal mirror.


Field intensity at a typical frequency in the gap and at a resonant frequency corresponding to a transmission spike.

Surface defect

The complex dispersion relation w=W(k) for real values of the wave vector from 0.401=W(0.0) to 0.327=W(0.5). There are evidently three points with Re(W(k))=0, corresponding to nonrobust guided modes and a dispersion relation starting at k=0.344 for robust guided modes.


A nonrobust guided mode at k=0.0, w=0.401.


A robust guided mode at k=0.50, w=0.327.


Scattered field at k=0.0, w=0.271.


Scattered field at k=0.23, w=0.368, near a nonrobust guided mode.



Random crystals

The numbers in parentheses refer to the ratio of the maximal intensity of the field compared to the intensity of the incident field.

Perfect 1x10 supercell

1. (1.12)
2. (1.32)
3. (1.48)
4. (1.47)
5. (2.01)
6. (4.17)
7. (3.00)
8. (1.96)
9. (4.48)
10. (2.16)
11. (2.17)
12. (2.70)

1x10 supercell with 10% random perturbations of centers

1. (9.80)
2. (43.84)
3. (2.16)

1x10 supercell with 20% random perturbations of centers

1. (25.85)
2. (2.51)
3. (5.40)

1x10 supercell with 20% random perturbations of centers

1. (7.91)
2. (35.88)
3. (40.49)

1x10 supercell with 30% random perturbations of centers

1. (36.17)
2. (14.59)
3. (8.43)

1x10 supercell with 30% random perturbations of centers

1. (3.42)
2. (57.62)
3. (16.04)

1x10 supercell with 10% random perturbations of radii

1. (12.66)
2. (14.09)
3. (11.07)

1x10 supercell with 30% random perturbations of radii

1. (7.26)
2. (23.26)
3. (4.99)

1x10 supercell with 30% random perturbations of radii

1. (5.52)
2. (2.43)
3. (5.52)

1x10 supercell with 50% random perturbations of radii

1. (4.62)
2. (2.00)
3. (3.32)
4. (21.05)
5. (6.06)
6. (9.91)

1x10 supercell with 50% random perturbations of radii

1. (1.23)
2. (25.23)
3. (25.61)
4. (5.53)
5. (31.62)
6. (25.82)

5x5 supercell, 30% random perturbations of centers, 30° angle of incidence
(11.03)