LaSIP Workshop on Assessing Standards-Based Learning

Director’s Introduction to the Assessment Modules

James J. Madden, Department of Mathematics, LSU Baton Rouge

This essay explains what we mean by an "assessment module" and then goes on to describe how the participants in this workshop went about creating their own assessment modules. We encourage visitors to read this introduction before looking at the posted work.

In this workshop, our chief goal was to become more effective users of Investigations in Number, Data and Space, a well-known and highly respected mathematics curriculum for grades K-5. In consonance with the guiding philosophy of Investigations, we planned to achieve this goal by studying both the mathematical content in the curriculum as well as the ways that children develop their own understandings of that content.

The science of learning informs us of the general patterns by which learning occurs. Assessment informs us how those whom we are teaching advance through the stages of mastery. We sought to refine some of the assessment tools that are provided in Investigations — and even develop our own original assessment tools — using the conceptual framework for assessment that was put forward in the National Research Council report Knowing What Students Know (2001). By this process, we expected both to learn about assessment and to create final products that we could share with one another and that other teachers outside our group might find useful as well.

The Workshop Home Page includes a statement of the goals with which we began our workshop. There is, in fact, a subtle difference between what we envisioned at the outset and what I think we have accomplished. As I look back. I see that all of us — directors, staff and participants — grew not only in our understanding of content and pedagogy, but also in our ability to share ideas about these things with one another. Ultimately, the entire workshop became an exchange among over 30 genuine experts with various specialties. It was not a presentation by a few “special experts” claiming some privileged knowledge. It was a partnership, in which we all learned from one another. In retrospect there could have been no better goal. We became a learning community, in which new teaching-centered ideas about mathematics assessment were created and shared by all. Arguably, we achieved what TIMSS researchers James Stigler and James Hiebert wrote about so approvingly in The Teaching Gap:

In a true profession, the wisdom of the professions's members finds its way into the most common methods. The best that we know becomes the standard of doing something. The star teachers of the twenty-first century will be teachers who work every day to improve teaching---not only their own but that of the whole profession.

The Assessment Triangle

Assessment is the only means by which we can learn about the ways that children develop knowledge and understanding. It is the only window we have into students’ minds. In the preparing the report Knowing What Students Know, the National Research Council Committee on the Foundations of Assessment set out to “rethink the fundamental scientific principles and philosophical assumptions serving as the foundations for current approaches to assessment.” (page 1). A main conclusion of this report is that educational assessments at all levels can and should be based on scientifically validated models of cognition and learning. Yet, the report asserts, in most educational settings at present we are nowhere near realizing this goal. Not only do we know little about the ways people learn, we also lack the instruments that enable us to observe the learning process in any meaningful way.

As a conceptual framework for thinking about assessment, the NRC committee put forward the so-called assessment triangle. This schematizes the way that cognitive models are incorporated in the assessment process. The three corners of the triangle are (1) a model of student cognition in the specific domain to be assessed, (2) a method of evoking, observing and recording behaviors that provide evidence of students’ competencies and (3) an interpretive process for making sense of the recorded evidence:

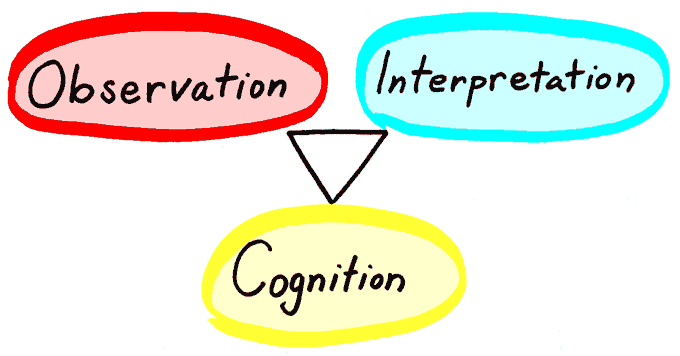
To find out more about the triangle, click on the parts.

The assessment triangle is a high-level model of what we do when we assess student learning. It is also an implicit recommendation for how to design, describe and evaluate assessment tools. The model is general enough to encompass instruments used for a variety of purposes and at numerous levels, including:

• direct interactions between students and teachers during the course of instruction for the purpose of tailoring instruction and monitoring and pacing individual learning,
• cumulative reports on individual student progress prepared for parents, schools or other authorities,
• standardized testing (used for a variety of purposes—not always mutually compatible),
• large-scale assessment undertaken to measure and compare the effectiveness of institutions and programs.

Implementing the Assessment Triangle

In our workshop, teams of K-5 teachers who were becoming familiar with the Investigations curriculum took the assessment triangle as a template and used it to design assessment instruments to support their classroom practice. I want to describe how the assessment triangle was translated into specific working goals that the teams used as they designed, developed and tested their own assessment tools. Let me jump into the middle by presenting a couple of examples based on an actual work by teacher teams.

Example 1. Most Kindergartners are able to recognize, build and describe designs that incorporate repetitive patters of various kinds. For example, they notice patterns, such as red-black-red-black-etc. or red-red-black-red-red-black-etc., of beads on a string. They also describe such patterns in words, copy them and extend them (e.g., by adding more beads to the string in the proper order) and they make up their own patterns. The ability to work with repetitive patterns is probably a complex cognitive skill with many components. To assess what parts of this skill children possessed, our Kindergarten team asked children to work with colored paper squares on a number of different tasks (including copying patterns from templates, continuing or extending patterns, transforming patterns from one format to another, providing symbolic descriptions of patterns, comparing patterns in different formats, describing the respects in which different patterns resemble one another, and making up a variety of new and different patterns and classifying them). Comparing the performances of several children, the team noticed that certain abilities were widespread while others were less common. They began to develop a landscape in which each child occupied a position based on the particular abilities in this domain that he or she had. Ultimately, the team was able to provide characterizations of the different kinds of competence that children demonstrate and make recommendations to teachers as to how to respond to such differences when they have specific learning goals in mind. For more information, see the Kindergarten Module.

Example 2. Arithmetic abilities consist of interrelated parts, including specific factual knowledge (such as the multiplication table), the ability to link this knowledge to appropriate situations and the ability to use it in performing complex procedures. Many studies have demonstrated that different components may be acquired independently. Some children, for example, learn formal multiplication facts without acquiring a deep grasp of their meaning. One 3rd-grade teacher team decided to acquire information about how children understand the meaning of multiplication by asking them to make up stories that involve multiplication. When responding to this assignment, some students imagined situations that clearly modeled multiplication. For example, one child wrote about tomato attacks in a distant land (a place rife with ham actors, perhaps). There were 3 tomatoes in each attack, and the attacks occurred on 4 consecutive days, so all together 12 tomatoes fell. Such work constitutes evidence of a grasp of the meaning of multiplication. This is not stand-alone evidence, to be sure, but it might be combined with other sources of information to create a picture of what the student understands. This particular story suggests that the state of the student's understanding probably conforms to what would be deemed desirable in many modern curricula. On the other hand, some students wrote stories in which two numbers appeared and then got multiplied for no apparent reason other than to satisfy the imposed requirement that the story be about multiplication. For example, one student wrote about a bunny that had 2 Easter eggs and then later got 8 more. So he multiplied 2 and 8 and had 16 eggs. Several other students produced similar work, in which multiplication was either meaningless or inappropriate. While this kind of work certainly raises a red flag, a single paper like this might not mean anything. As we questioned the students, we found that answers like this were not necessarily symptoms of deep misunderstandings. In some cases, they may have resulted from carelessness, possibly due to a lack of interest in the particular assignment. Before drawing a conclusion, one would want to gather additional information. (Go to Grade 3 Module A.)

To be continued...