We owe the T-shirt design and our 2013 contest logo to Prof. Stephen Shipman of LSU Math Department, his sister, Barbara Shipman, and brother, Patrick Shipman.

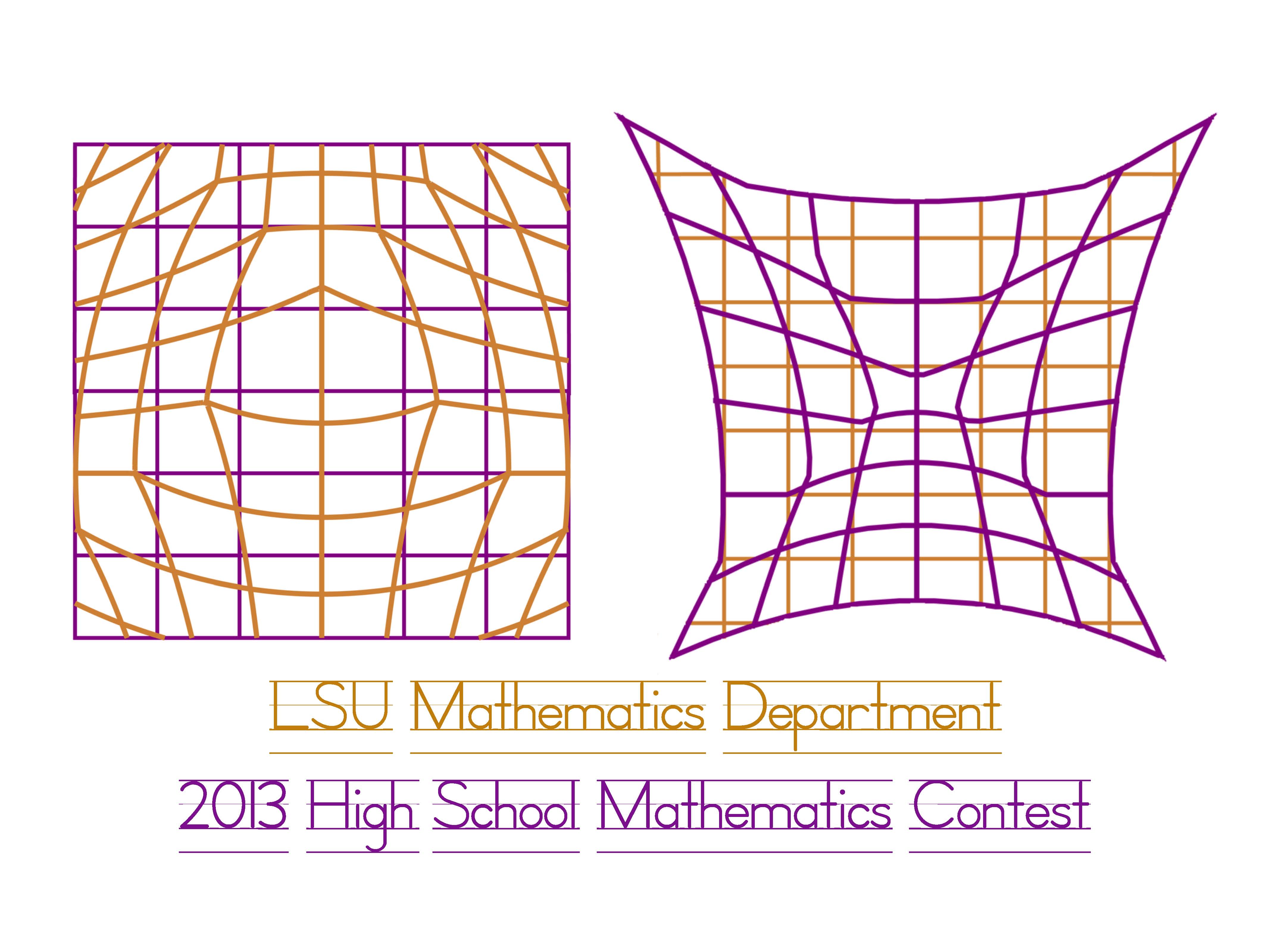
This is a nonlinear map (the tiger-trophy map) that preserves Lorentz orthogonality. Two lines are called Lorentz-orthogonal if they are reflections of one another about the 45-degree line. Each pair of vertical and horizontal purple lines on the left is mapped to a pair of purple curves on the right that intersect Lorentz-orthogonally. Likewise, each pair of vertical and horizontal gold lines on the right is mapped back to a pair of gold curves that intersect Lorentz-orthogonally. There are some non-smooth points in the image curve of each straight line, where the curve has two different tangent lines. For Lorentz orthogonality one must use a tangent line whose slope in null-line coordinates is the harmonic average of the right and left slopes. This image depicts part of a Lorentz-orthogonal bijection of the whole plane to itself. Designed by Barbara Shipman, Patrick Shipman and Stephen Shipman.